*** Un peu de géométrie (2)

On considère un rectangle \(\text A\text B\text C\text D\) tel que \(\text A\text B=8\) et \(\text A\text D=4\).
Soit \(\text M\) le point de  \([\text A\text B]\)  tel que \(\text A\text M=x\).
On construit le triangle \(\text M\text B\text C\) et le demi-cercle de diamètre \([\text A\text M]\) inclus dans le rectangle \(\text A\text B\text C\text D\).
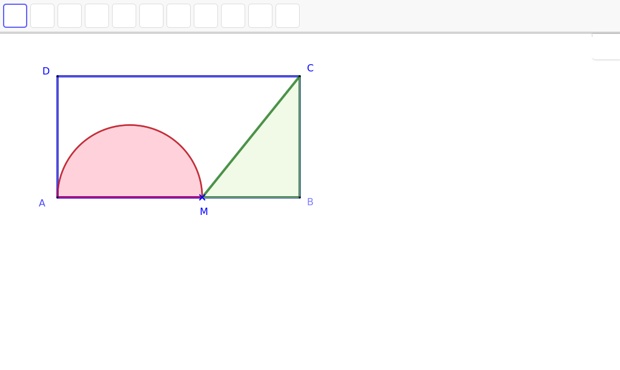
On représente la situation ci-dessous. 
Sur la figure ci-dessous, vous pouvez déplacer le point \(\text M\) sur le segment \([\text A\text B]\) pour modéliser la situation.

1. On chercher à déterminer l'aire \(\mathcal{A}_{\text M\text B\text C}(x)\)du triangle \(\text M\text B\text C\) en fonction de \(x\).
    a. Exprimer la longueur \(\text M\text B\) en fonction de \(x\).
    b. En déduire l'expression de \(\mathcal{A}_{\text M\text B\text C}(x)\).
2. Exprimer maintenant l'aire \(\mathcal{A}_{1}(x)\) du demi-cercle de diamètre \([\text A\text M]\) en fonction de \(x\).
3. À l'aide de la calculatrice, donner une valeur approchée de \(x\) telle que l'aire \(\mathcal{A}_{\text M\text B\text C}(x)\) du triangle \(\text M\text B\text C\) soit égale à l'air e \(\mathcal{A}_{1}(x)\) du demi-cercle de diamètre \([\text A\text M]\).